52. N-Queens II

发表于 | 分类于 | 阅读次数
字数统计 1,257 | 阅读时长 6

52. N - Queens II

Follow up for N-Queens problem.

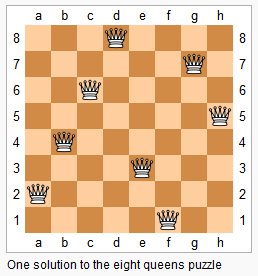
52-8-queens

Now, instead outputting board configurations, return the total number of distinct solutions.

题意：

　　跟进的N皇后问题。现在，N皇后的输出板配置，返回不同解决方案的总数。

思路：

　　此题其实和51. N - Queens是同一个题，不同的地方是51. N - Queens是求所有的结果集返回，此题要求的是求得结果集的个数，也有三种方法，具体思路见51. N - Queens。

　方法一：

　　递归回溯，同51. N - Queens方法一。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
	int totalNQueens(int n) {
		vector<int> check(n, 0);
		int counts = 0;//用来记录结果集的个数
		placeQueens(counts, check, 0, n);
		return counts;
	}
	void placeQueens(int &counts, vector<int> check,int row, int n) {
		if (row>n-1)
		{
			counts++;
			return;
		}
		for (int j = 0;j<n;j++)
		{
			if (placeIsValid(check,row,j))
			{
				check[row] = j;
				placeQueens(counts, check, row + 1, n);
			}
		}
	}
	int placeIsValid(vector<int> check, int row, int col) {
		for (int i = 0; i < row; i++)
		{
			if (check[i]==col||abs(check[i]-col)==abs(i-row))
			{
				return 0;
			}
		}
		return 1;
	}
};

　方法二：

　　非递归实现，同51. N - Queens方法二。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class Solution3 {
public:
	int totalNQueens(int n) {
		vector<int> check(n, INT_MIN);
		int counts = 0;
		int i = 0, j = 0;
		while (i<n)
		{
			while (j<n)
			{
				if (placeIsValid(check,i,j))
				{
					check[i] = j;
					j = 0;//第i行放置皇后以后，需要继续探测下一行的皇后位置，所以此处将j清零，从下一行的第0列开始逐列探测  !!!!!!!!!!!!!!!!!
					break;
				}
				else
				{
					j++;
				}
			}
			if (check[i]==INT_MIN)
			{
				if (i==0)
				{
					break;
				}
				else
				{
					i--;
					j = check[i] + 1;
					check[i] = INT_MIN;
					continue;
				}
			}
			if (i == n-1)
			{
				counts++;

				j = check[i] + 1;
				check[i] = INT_MIN;
				continue;
			}
			i++;
		}
		return counts;
	}
	int placeIsValid(vector<int> check, int row, int col) {
		for (int i = 0; i < row; i++)
		{
			if (check[i] == col || abs(check[i] - col) == abs(i - row))
			{
				return 0;
			}
		}
		return 1;
	}
};

　方法三：

　　递归回溯位运算实现，同51. N - Queens方法三。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
public:
	int counts = 0;
	int upperLimit = 1;
 	int totalNQueens(int n) {
		upperLimit = (upperLimit << n) - 1;
		placeQueens(0, 0, 0);
		return counts;
	}
	void placeQueens(int row, int lXie, int rXie)
	{
		if (row==upperLimit)//row是记录每一行的列位置皇后，当等于upperLimit最大限制的时候说明找到一个满足条件的皇后矩阵
		{
			counts++;
			return;
		}
		//~按位取反    ^按位异或
		int pos = upperLimit&~(row | lXie | rXie);//获取此时行的所有可插入皇后的位置
		while (pos)//pos不为0说明肯定有位置可以放皇后
		{
			//这个地方思想是按位取反加1，然后为了取到最右面的1必须与原pos相与，如果按自己下面的想法没有相与，导致出错
			//int p = pos;
			//p = ~p + 1;//先确定能放在此行的最右面的皇后的位置p
			//可以改为形式1
			int p = pos & (~pos + 1);

			// 拷贝pos最右边为1的bit，其余bit置0  
			// 也就是取得可以放皇后的最右边的列  
			//可以改为形式2
			/*pos & -pos 的意思就是取最右边的 1 再组成二进制数，相当于 pos &（~pos + 1），因为取反以后刚好所有数都是相反的（怎么听着像废话），再加 1 ，就是改变最低位，如果低位的几个数都是1，加的这个 1 就会进上去，一直进到 0 ，在做与运算就和原数对应的 1 重合了。举例可以说明：

				原数 0 0 0 0 1 0 0 0    原数 0 1 0 1 0 0 1 1
				取反 1 1 1 1 0 1 1 1    取反 1 0 1 0 1 1 0 0
				加1    1 1 1 1 1 0 0 0    加1  1 0 1 0 1 1 0 1
				与运算    0 0 0 0 1 0 0 0 and 0 0 0 0 0 0 0 1
				其中呢，这个取反再加 1 就是补码，and 运算 与负数，就是按位和补码与运算。*/
			//long p = pos & -pos;   //p记录的是可以放皇后的最右面的一个                                             

								   // 将pos最右边为1的bit清零  
								   // 也就是为获取下一次的最右可用列使用做准备，  
								   // 程序将来会回溯到这个位置继续试探  
			pos -= p;         //去掉最右面一个选取的位置，进行递归判断下一个最右面皇后的位置        

			placeQueens(row + p, (lXie + p) << 1, (rXie + p) >> 1);
		}
	}
};

　Java Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    public int totalNQueens(int n) {
        if (n == 0) {
            return 0;
        }

        int[] rowCheck = new int[n];
        int res = placeQueens(n, 0, rowCheck);
        return res;
    }

    public int placeQueens(int n, int row, int[] rowCheck) {
        if (row == n) {
            //res += 1;
            return 1;
        }

        int res = 0;
        for (int j = 0;j < n;j++) {
            if (checkValid(row, j, rowCheck)) {
                rowCheck[row] = j;
                res += placeQueens(n, row + 1, rowCheck);
            }
        }
        return res;
    }

    public boolean checkValid(int row, int col, int[] rowCheck) {
        for (int i = 0;i < row;i++) {
            if (rowCheck[i] == col || Math.abs(row - i) == Math.abs(rowCheck[i] - col)) {
                return false;
            }
        }

        return true;
    }
}