62. Unique Paths

发表于 | 分类于 | 阅读次数
字数统计 412 | 阅读时长 2

62. Unique Paths

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).
How many possible unique paths are there?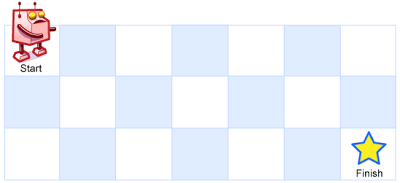
62-robot_maze
Above is a 3 x 7 grid. How many possible unique paths are there?
Note: m and n will be at most 100.

题意：

　　一个机器人位于一个m*n网格的左上角（下图中标有“开始”）。机器人在坐标点方格内只能向下或向右移动。机器人正试图到达网格的右下角（下图中标有“完成”）。求有多少种可能的路径？

思路：

　　动态规划，用一个辅助矩阵dp，矩阵元素值来记录到达这个单元格的所有路径条数，到达每一个单元格只能从左边或者上边到达，所以此单元格的路径数等于左边和上边单元格元素的和，所以动态转移方程：dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
	int uniquePaths(int m, int n) {
		vector<vector<int>> dp(m, vector<int>(n, 1));
		for (int i =1;i<m;i++)
		{
			for (int j = 1;j<n;j++)
			{
				dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
			}
		}
		return dp[m-1][n-1];
	}
};

　Java Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int uniquePaths(int m, int n) {
        if (m == 0 || n == 0) {
            return 0;
        }

        int[][] res = new int[m][n];
        int[] vals = new int[n];
        Arrays.fill(vals, 1);
        Arrays.fill(res, vals);

        for (int i = 1;i < m;i++) {
            for (int j = 1;j < n;j++) {
                res[i][j] = res[i - 1][j] + res[i][j - 1];
            }
        }

        return res[m - 1][n - 1];
    }
}