72. Edit Distance

Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.)

You have the following 3 operations permitted on a word:
a) Insert a character
b) Delete a character
c) Replace a character

题意：

　　 给定两个单词word1 word2和，找到从word1转换到word2需要转换到的最小步数。（每一次操作算为1步。）

　　 有以下3个字所允许的操作：
　　 　　 a）插入字符
　　 　　 b）删除字符
　　 　　 c）替换字符

思路：

　　本题是典型的适合使用动态规划的题目。如果要计算单词”INTENTION”和单词”EXECUTION”之间的编辑距离，首先，把这个问题简单化。把上面两个单词简化为长度为1的两个单词I和E。
　　1) 如果要“I”变化为”E”，可以把”I”替换为”E”
　　2) 如果要“I”变化为空串” “，可以把”I”删除，从而形成””
　　3) 如果要空串“ ”变化为”E”，可以把”E”插入，从而形成E
　　上面三种变化分别表示替换，删除，插入这三种基本操作。
　　接下来，定义一个表达式D(i,j)。它表示从第1个字单词的第0位至第i位形成的子串和第2个单词的第0位至第j位形成的子串的编辑距离。
　　显然，可以计算出动态规划的初始表达式，如下:
　　　　D(i,0) = i
　　　　D(0,j) = j
　　然后，考虑动态规划的状态转移方程式，如下: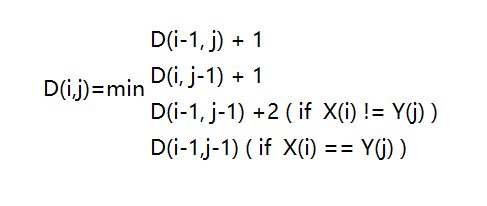

　　上面的状态转移方程的含义是，D(i,j)的值，要么是D(i-1, j)的操作完成之后删除一个字符(第1个单词的第i个字符)，要么是D(i, j-1)的操作完成之后增加一个字符(第2个单词的第j个字符)，要么是D(i-1, j-1)的操作完成之后替换一个字符(如果第1个单词的第i个字符和第2个单词的第j个字符不等)，或者是D(i-1, j-1)的操作完成之后什么也不做(如果第1个单词的第i个字符和第2个单词的第j个字符相等)。其中，下图定义删除，插入，替换的操作步数分别为一步，一步，两步。
　　以第一个单词”INTENTION”和第二个单词”EXECUTION”为例，看下面的图

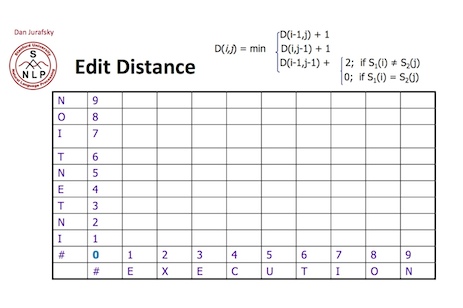
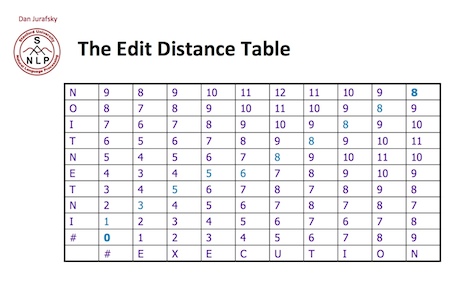
　　注意在此题中，把插入，删除，替换全部定义为一步操作。

class Solution {
public:
	int minDistance(string word1, string word2) {
		int word1Size = word1.size();
		int word2Size = word2.size();
		vector <vector<int>> dp(word1Size + 1, vector<int>(word2Size+1, 0));
		for (int i = 0;i<word1Size+1;i++)
		{
			dp[i][0] = i;
		}
		for (int j = 0; j < word2Size + 1; j++)
		{
			dp[0][j] = j;
		}
		for (int i = 1;i<word1Size+1;i++)
		{
			for (int j = 1;j<word2Size+1;j++)
			{
				if (word1[i - 1] == word2[j - 1])
				{
					dp[i][j] = dp[i - 1][j - 1];
				}
				else
					dp[i][j] = dp[i - 1][j - 1] + 1;
				int tempDp = min(dp[i - 1][j] + 1,dp[i][j-1]+1);
				dp[i][j] = min(dp[i][j], tempDp);
			}
		}
		/*
		for (int i = 0; i < word1Size + 1; i++)
		{
			for (int j = 0; j < word2Size + 1; j++)
			{
				cout << dp[i][j] << " ";
			}
			cout << endl;
		}
		*/
		return dp[word1Size][word2Size];
	}
};