87. Scramble String

发表于 | 分类于 | 阅读次数
字数统计 1,609 | 阅读时长 7

87. Scramble String

Given a string s1, we may represent it as a binary tree by partitioning it to two non-empty substrings recursively.
Below is one possible representation of s1 = “great”:

87-1-Scramble-String

To scramble the string, we may choose any non-leaf node and swap its two children.

For example, if we choose the node “gr” and swap its two children, it produces a scrambled string “rgeat”.

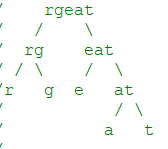
87-2-Scramble-String

We say that “rgeat” is a scrambled string of “great”.

Similarly, if we continue to swap the children of nodes “eat” and “at”, it produces a scrambled string “rgtae”.

87-3-Scramble-String

We say that “rgtae” is a scrambled string of “great”.
Given two strings s1 and s2 of the same length, determine if s2 is a scrambled string of s1.

题意：

　　给定一个字符串S1，我们可以将其表示为一个二叉树划分为两个非空的子字符串递归。
　　Scramble String，我们可以选择任何非叶节点并交换它的两个孩子。

思路：

　方法一：

　　 这道题的要求是判断两个字符串是否是Scramble String。如果两个字符串是Scramble String，则其长度必然相等。而且，在某位置切开s1，则s1左侧与s2左侧相同数量的子串为Scramble String，并且s1右侧与s2右侧相同数量的子串为Scramble String；或者s1左侧与s2右侧相同数量的子串为Scramble String，并且s1右侧与s2左侧相同数量的子串为Scramble String。
思路有了，就可以通过递归调用遍历每组分割点了。其中a1和b1分别表示s1中以a1开始b1结束的子串，a2和b2分别表示s2中以a2开始b2结束的子串。

利用递归的思想,有三种情况需要考虑：

  1. 如果两个substring相等的话，则为true
  2. 如果两个substring中间某一个点，左边的substrings为scramble string，同时右边的substrings也为scramble string，则为true
  3. 如果两个substring中间某一个点，s1左边的substring和s2右边的substring为scramble string, 同时s1右边substring和s2左边的substring也为scramble string，则为true
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
	bool isScramble(string s1, string s2) {
		if (s1==s2)
		{
			return true;
		}
		if (s1.size()!=s2.size())
		{
			return false;
		}
		vector<int> hash(26, 0);
         // 剪枝，如果子串中的字符不同，则必然不是Scramble String，不用再进行分割处理了
		for (int i = 0;i<s1.size();i++)//此处利用计数法判断两个字符串中的字符是否是都相等的
		{
			hash[s1[i] - 'a']++;
			hash[s2[i] - 'a']--;
		}	
		for (int i = 0; i < 26; i++)
		{
			if (hash[i] != 0)//只要有一个元素不为0，说明就有字符不相同
				return false;
		}
		for (int len =1;len<s1.size();len++)
		{
			if ( isScramble(s1.substr(0,len),s2.substr(0,len))&&isScramble(s1.substr(len),s2.substr(len)) || isScramble(s1.substr(0, len), s2.substr(s1.size()-len)) && isScramble(s1.substr(len), s2.substr(0,s1.size()-len))  )
			{
				return true;
			}
		}
		return false;
	}
};

　方法二：

　　 利用动态规划的思想解题，这其实是一道三维动态规划的题目，我们提出维护量res[i][j][n]，其中i是s1的起始字符，j是s2的起始字符，而n是当前的字符串长度，res[i][j][len]表示的是以i和j分别为s1和s2起点的长度为len的字符串是不是互为scramble。
　　有了维护量我们接下来看看递推式，也就是怎么根据历史信息来得到res[i][j][len]。判断这个是不是满足，其实我们首先是把当前s1[i…i+len-1]字符串劈一刀分成两部分，然后分两种情况：
　　　　第一种是左边和s2[j…j+len-1]左边部分是不是scramble，以及右边和s2[j…j+len-1]右边部分是不是scramble；
　　　　第二种情况是左边和s2[j…j+len-1]右边部分是不是scramble，以及右边和s2[j…j+len-1]左边部分是不是scramble。
　　如果以上两种情况有一种成立，说明s1[i…i+len-1]和s2[j…j+len-1]是scramble的。而对于判断这些左右部分是不是scramble我们是有历史信息的，因为长度小于n的所有情况我们都在前面求解过了（也就是长度是最外层循环）。
　　上面说的是劈一刀的情况，对于s1[i…i+len-1]我们有len-1种劈法，在这些劈法中只要有一种成立，那么两个串就是scramble的。
　　总结起来递推式是res[i][j][len] ||= (res[i][j][k]&&res[i+k][j+k][len-k] || res[i][j+len-k][k]&&res[i+k][j][len-k]) 对于所有1<=k<len，也就是对于所有len-1种劈法的结果求或运算。因为信息都是计算过的，对于每种劈法只需要常量操作即可完成，因此求解递推式是需要O(len)（因为len-1种劈法）。
　　如此总时间复杂度因为是三维动态规划，需要三层循环，加上每一步需要线行时间求解递推式，所以是O(n^4)。虽然已经比较高了，但是至少不是指数量级的，动态规划还是有很大有事的，空间复杂度是O(n^3)
　　维护变量dp[i][j][len]，其中i是s1的起始字符，j是s2的起始字符，而n是当前的字符串长度，表示的是以i和j分别为s1和s2起点的长度为len的字符串是不是互为Scramble String。
　　递推公式也是前面的思路：dp[i][j][len] ||= (dp[i][j][k]&&dp[i+k][j+k][len-k] || dp[i][j+len-k][k]&&dp[i+k][j][len-k])。和方法一不同之处就是把前面的结果都记录下来，根据前面的结果集去计算当前结果，并不像一中用递归计算，这是动态规划的显著特征，用空间换时间，用已经计算的值来求当前值，减少计算时间复杂度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
	bool isScramble(string s1, string s2) {
		if (s1 == s2)
		{
			return true;
		}
		int s1Len = s1.size();
		int s2Len = s2.size();
		if (s1.size() != s2.size())
		{
			return false;
		}
		vector<vector<vector<bool>>> dp(s1Len, vector<vector<bool>>(s1Len, vector<bool>(s1Len + 1, false)));
		for (int i = 0;i<s1Len;i++)
		{
			for (int j = 0;j<s2Len;j++)
			{
				dp[i][j][1] = (s1[i] == s2[i]);
			}
		}
		for (int len = 2;len<=s1Len;len++)//截取串的长度
		{
			for (int i = 0; i <= s1Len - len; i++)
			{
				for (int j = 0; j <= s2Len-len; j++)
				{
					for (int k = 1;k<=len;k++)//k是一个串的左右分隔点
					{
						dp[i][j][k] = dp[i][j][k] || dp[i][j][k] && dp[i + k][j + k][len-k] || dp[i][j + len - k][k] && dp[i + len - k][j][k];
					}
				}
			}
		}
		return dp[0][0][s1Len];
	}
};