95. Unique Binary Search Trees II

发表于 | 分类于 | 阅读次数
字数统计 601 | 阅读时长 3

95. Unique Binary Search Trees II

Given an integer n, generate all structurally unique BST’s (binary search trees) that store values 1…n.

For example,
Given n = 3, your program should return all 5 unique BST’s shown below.

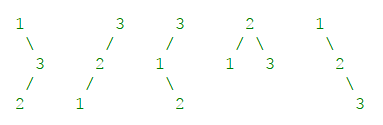
95-Unique Binary Search Trees II

题意：

　　给定一个整数n，生成所有结构不同的的BST（二分搜索树），存储值为1…n。

思路：

　　这题是 96 Unique Binary Search Trees 的延展，它已经不是让求不同构二叉树的种数，而是直接给出这些不同构的二叉树。

  1. 每一次都在一个范围内随机选取一个结点作为根。
  2. 每选取一个结点作为根，就把树切分成左右两个子树，直至该结点左右子树为空。

　　大致思路如上，可以看出这也是一个可以划分成子问题求解的题目，所以考点是动态规划。
　　但具体对于本题来说，采取的是自底向上的求解过程。

  1. 选出根结点后应该先分别求解该根的左右子树集合，也就是根的左子树有若干种，它们组成左子树集合，根的右子树有若干种，它们组成右子树集合。
  2. 然后将左右子树相互配对，每一个左子树都与所有右子树匹配，每一个右子树都与所有的左子树匹配。然后将两个子树插在根结点上。
  3. 最后，把根结点放入链表中。

　　由于1~n是升序列，因此建起来的树天然就是BST。
　　递归思想，依次选择根节点，对左右子序列再分别建树。
　　由于左右子序列建树的结果也可能不止一种，需要考虑所有搭配情况。
　　vector left代表所有valid左子树。
　　vector right代表所有valid右子树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
	vector<TreeNode*> generateTrees(int n) {
		vector<TreeNode*> res;
		res = createTrees(1, n);
		return res;
	}
	vector<TreeNode*> createTrees(int begin, int end) {
		vector<TreeNode*> res;
		if (begin > end)
			res.push_back(NULL);
		if (begin==end)
		{
			res.push_back(new TreeNode(begin));
		}
		else {
			for (int i = begin;i<=end;i++)
			{
				vector<TreeNode*> leftTree = createTrees(begin, i - 1);//左子树集合
				vector<TreeNode*> rightTree = createTrees(i+1, end);//右子树集合
				for (int l = 0;l<leftTree.size();l++)
				{
					for (int r = 0;r<rightTree.size();r++)
					{
						TreeNode* root = new TreeNode(i);//根据本层i创建根节点
						root->left = leftTree[l];
						root->right = rightTree[r];
						res.push_back(root);
					}
				}
			}
		}
		return res;
	}
};