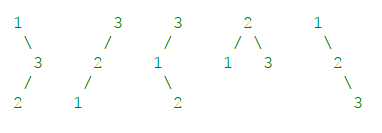96. Unique Binary Search Trees
Given n, how many structurally unique BST’s (binary search trees) that store values 1…n?
For example,
Given n = 3, there are a total of 5 unique BST’s.
题意:
给定一个整数n,计算可以生成多少个结构不同的的BST(二分搜索树),存储值为1…n。
思路:
分析:本题其实关键是递推过程的分析,n个点中每个点都可以作为root,当 i 作为root时,小于 i 的点都只能放在其左子树中,大于 i 的点只能放在右子树中,此时只需求出左、右子树各有多少种,二者相乘即为以 i 作为root时BST的总数。
递归过程中存在大量的重复计算,会超时,从n一层层往下递归,故考虑类似于动态规划的思想,让底层的计算结果能够被重复利用,故用一个数组存储中间计算结果(即 1~n-1 对应的BST数目),这样只需双层循环即可.
解题思路:
学数据结构的时候,曾学过不同构的二叉树的种数为卡特兰数,其通项公式如下:
1 | //卡特兰数通项公式 |
从求解子问题的角度来看本题:
- 选取一个结点为根,就把结点切成左右子树
- 以这个结点为根的可行二叉树数量就是左右子树可行二叉树数量的乘积
- 所以总的数量是将以所有结点为根的可行结果累加起来。也就是上述公式。
具体解法:
从C2开始求解,直到Cn,求解过的数依次存储在数组中,以备求解其后的元素使用。若使用递归,求解速度较慢。
时间上每次求解i个结点的二叉查找树数量的需要一个i步的循环,总体要求n次,所以总时间复杂度是O(1+2+…+n)=O(n^2)。空间上需要一个数组来维护,并且需要前i个的所有信息,所以是O(n)。
1 | class Solution { |